Entity groupings
We have taken the commonality by highest order such that grouping by pools takes precedence over node operators, which take precedence over deposit addresses.Interpreting the Gini
A Gini coefficient of 0 reflects perfect equality, where all income or wealth values are the same, while a Gini coefficient of 1 (or 100%) reflects maximal inequality among values.Gini calculation
Basing our calculation of the work by Evgeny Medvedev here, we first take thevalidator_count of each of the entities on the latest day and rank them in descending order accordingly. We then use the 1-2B formula for measuring the Gini, where B is the area under the Lorenz curve such that:
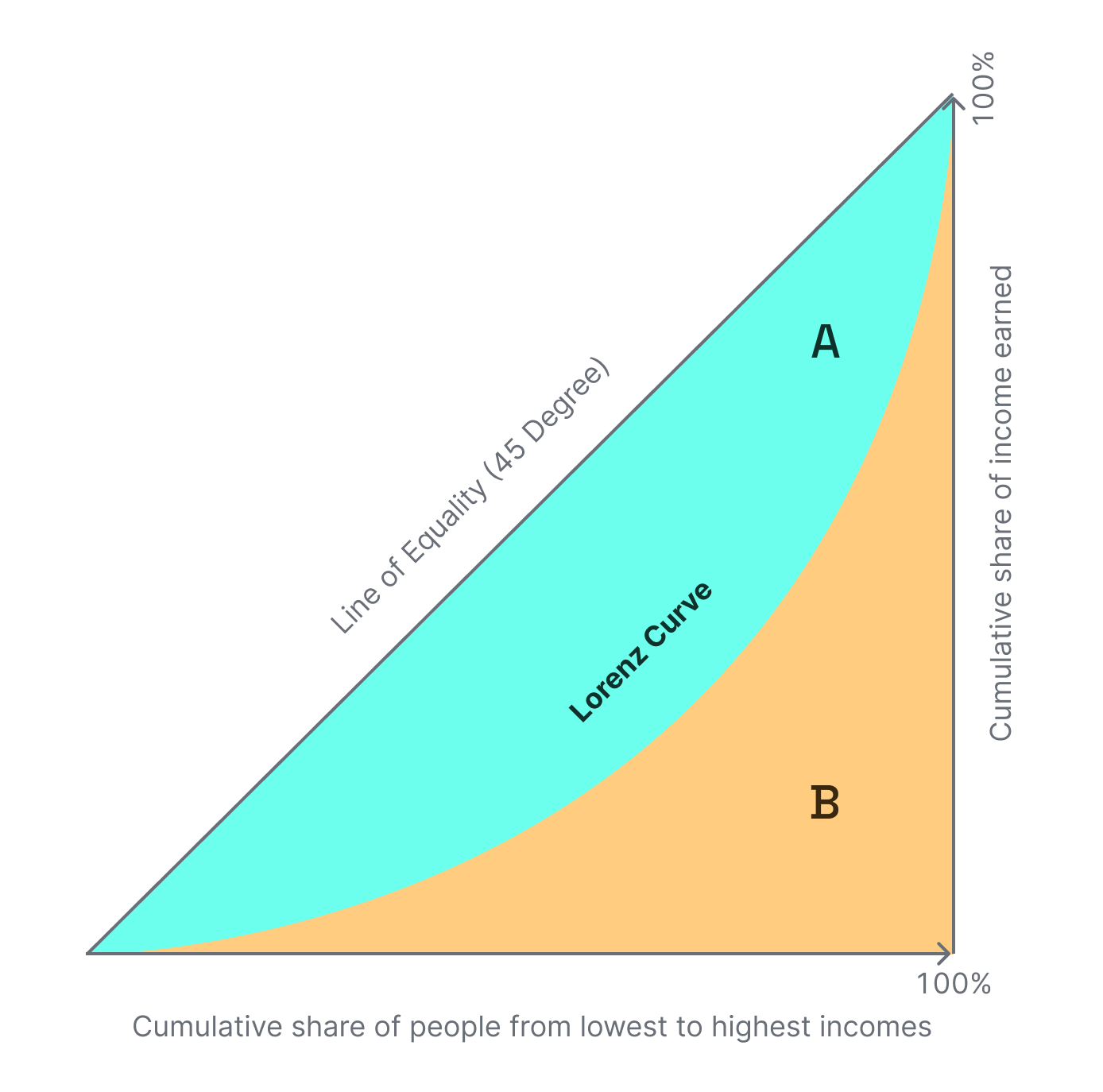
The shape of a Lorenz Curve.

