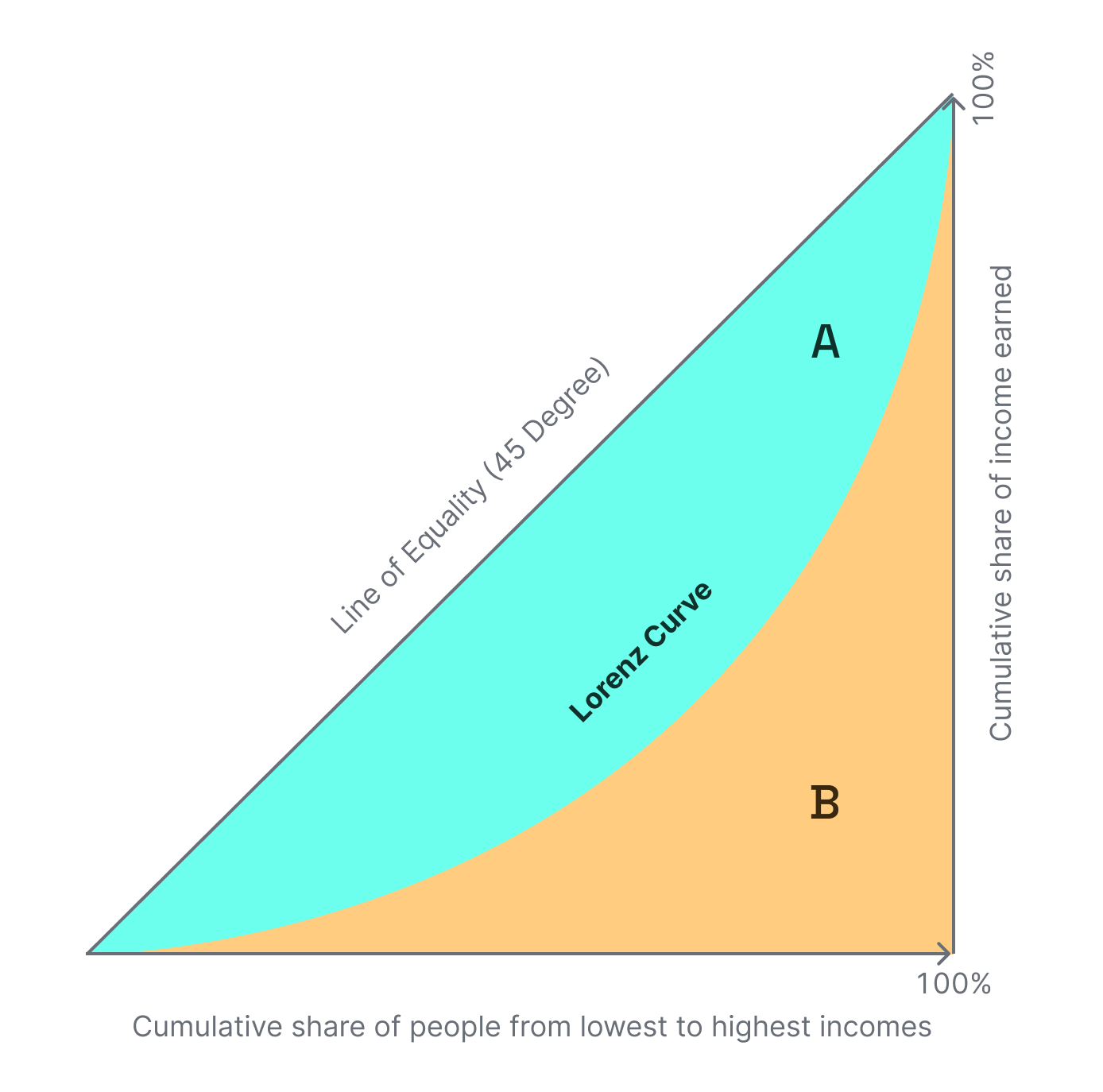
​
Interpreting the Gini

A Gini coefficient of 0 reflects perfect equality, where all income or wealth values are the same, while a Gini coefficient of 1 (or 100%) reflects maximal inequality among values.

​
Gini calculation

We first take the stake weight of each of the validators on the latest day and rank in descending order accordingly. We then use the 1-2B formula for measuring Gini, where B is the area under the Lorenz curve such that:
1−2×SUM(staked SOL×(rank−1)+staked SOL/2)COUNT(validators)×SUM(staked SOL)1 - 2 \times \frac{\text{SUM}(\text{staked SOL} \times (\text{rank} - 1) + \text{staked SOL} / 2)}{\text{COUNT(validators)} \times \text{SUM}(\text{staked SOL})}

The shape of a Lorenz Curve.

​
Function Components

staked SOL×(rank−1)\text{staked SOL} \times (\text{rank} - 1)
is the area of the rectangular horizontal slice under the Lorenz curve
staked SOL2\frac{\text{staked SOL}}{2}
is the area of the triangle on the left of the rectangular slice
SUM(staked SOL×(rank−1)+staked SOL2)\text{SUM}(\text{staked SOL} \times (\text{rank} - 1) + \frac{\text{staked SOL}}{2})
is the sum of all the slices
COUNT(validators)\text{COUNT(validators)}
normalizes the x axis to the range 0 to 1
SUM(staked SOL)\text{SUM}(\text{staked SOL})
normalizes the y axis to the range 0 to 1
SUM(staked SOL)\text{SUM}(\text{staked SOL})